Learn Bayesian Logistic regression from imbalanced data

Dataset

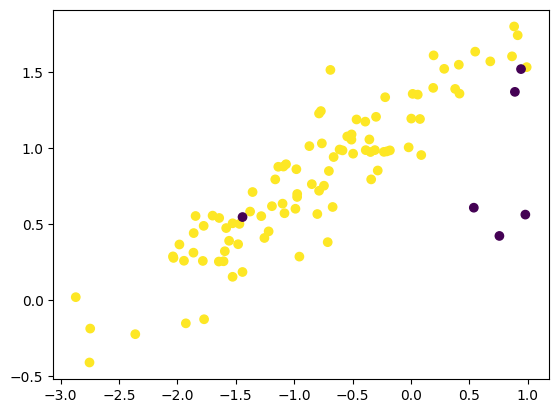
toy 2d dataset

Obviously, this is an imbalanced dataset. A dumb classifier may assign “yellow” to all points and yield apparently satisfactory accuracy.

Bayesian Logistic regression

Denote the $k$-th component of the softmax of $\boldsymbol z$ as:

\[\mathcal S_k(\boldsymbol z) \triangleq \frac{\exp(z_k)}{\sum_{k'}\exp(z_{k'})}\,.\]

The likelihood is:

\[p(y=k \mid \boldsymbol x, \mathbf W, \boldsymbol b) = \mathcal S_k(\mathbf W \boldsymbol x + \boldsymbol b)\,,\]

where matrix $\mathbf W$ consists of $K$ weight vector $\boldsymbol w_k \in \mathbb R^d$, $\boldsymbol x \in \mathbb R^d$, and $\boldsymbol b \in \mathbb R^K$.

For now, assign an uninformative Gaussian prior:

\[\forall k,\ \boldsymbol w_k \sim \mathcal N(0, \mathbf I)\,,\quad b_k \sim \mathcal N(0, 1)\,. \tag{1}\]

The posterior (given the dataset $\mathcal D$) is:

\[p(\mathbf W, \boldsymbol b \mid \mathcal D) \propto \prod_{k=1}^K p(\boldsymbol w_k) p(b_k) \prod_{j=1}^m p(y_j \mid \boldsymbol x_j, \mathbf W, \boldsymbol b)\,. \tag{2.1}\]

The predictive posterior is:

\[p(y \mid \boldsymbol x, \mathcal D) = \int p(y \mid \boldsymbol x, \mathbf W, \boldsymbol b) p(\mathbf W, \boldsymbol b \mid \mathcal D)\,\mathrm d \mathbf W \mathrm d \boldsymbol b\,. \tag{2.2}\]

Although both (2.1) and (2.2) are intractable, we may find $q(\mathbf W, \boldsymbol b) \approx p(\mathbf W, \boldsymbol b \mid \mathcal D)$ by variational inference, and estimate the predictive posterior by Monte Carlo after plugging in $q$. Since such procedure is out of scope, we won’t include details about it.

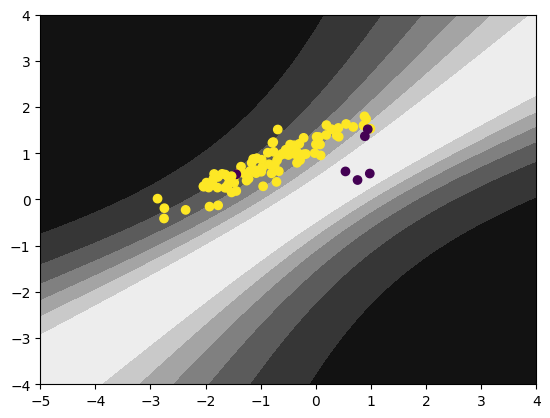
Let’s see the decision boundary and the uncertainty (measured by entropy) of the Bayesian LR:

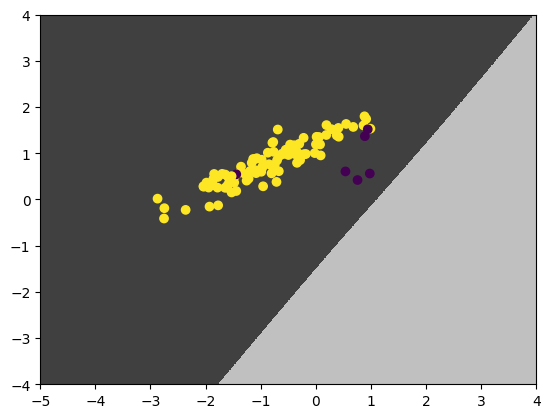
uninformative decision boundary

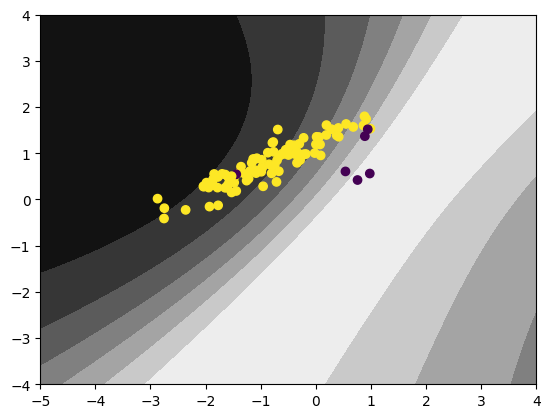
uninformative uncertainty

The model learns to be a dumb classifier!

We may apply rescaling (a.k.a. threshold shifting) to the learned classifier, by dividing the predictive posterior by the class prior (i.e. the proportion of samples of class $k$ in all samples), and use it to make prediction. The rescaled decision boundary and uncertainty are:

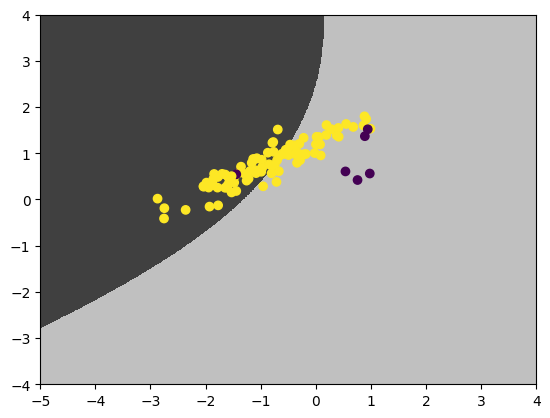
uninformative rescaled decision boundary

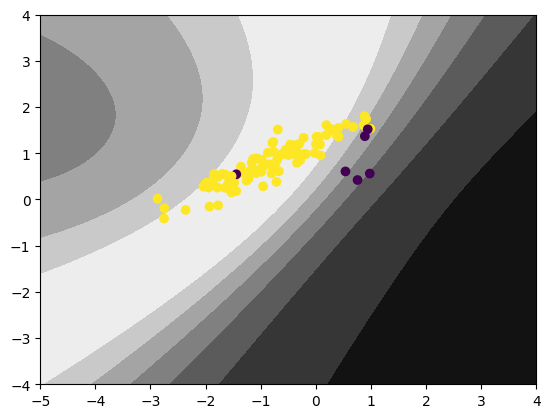
uninformative rescaled uncertainty

This benefits the minority class, but deteriorates the overall accuracy a lot.

Strengthen the prior

It turns out that if we strengthen the prior (by increasing its precision, or equivalently, decreasing its variance) of the intercepts in (1), things become much better. The new prior is:

\[\forall k,\ b_k \sim \mathcal N(0, 10^{-6})\,. \tag{3}\]

What we just encode into the prior reads:

I’m pretty sure that the two class weigh the same, despite the “purple” class appears inferior.

The result plots are:

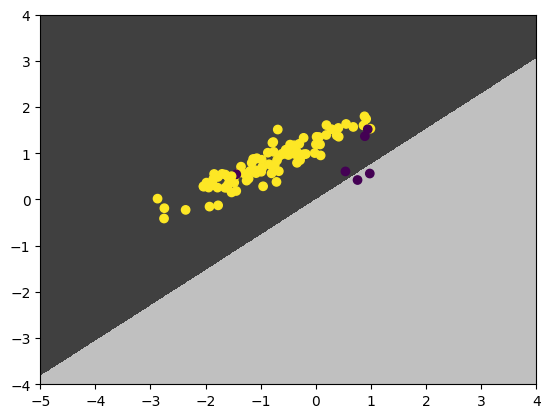
precise uninformative decision boundary

precise uninformative uncertainty

Bias the prior

What if we go further by biasing the classifier a little towards the minority class ($k=0$, “purple”)? The new prior is:

\[b_0 \sim \mathcal N(2, 10^{-6})\,,\quad b_1 \sim \mathcal N(0, 10^{-6})\,. \tag{4}\]

This prior reads:

I’m pretty sure there’re even a bit more “purple” class than “yellow” class a priori, despite they’re not sampled as much in the dataset.

The plots are now:

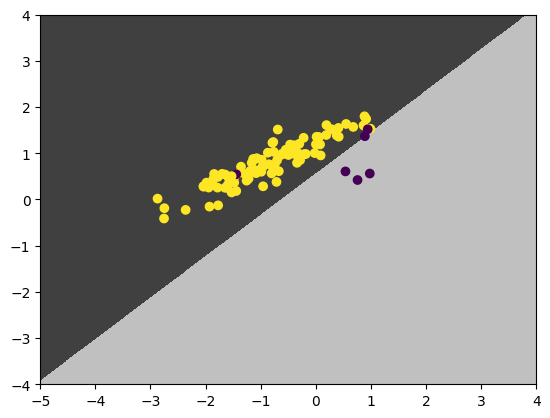
precise biased decision boundary

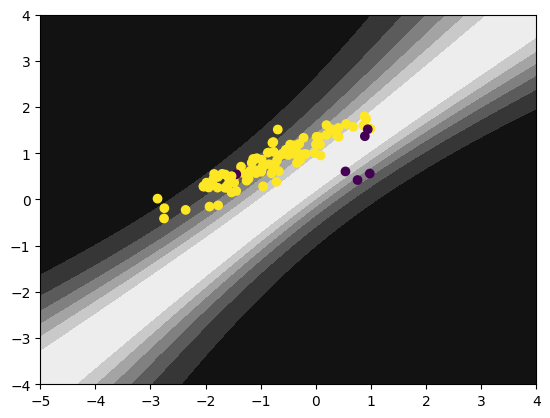
precise biased uncertainty

Pefect!

Conclusion

In this post, we see that under Bayesian framework, Bayesian LR is able to naturally combat imbalanced dataset by adjusting its prior belief.

This codebase generates all the figures in the post.

Appendix

Features and labels of the toy dataset.

The features:

array([[-0.46601866,  1.18801609],
       [ 0.53858625,  0.60716392],
       [-0.97431137,  0.69753311],
       [-1.09220402,  0.87799492],
       [-2.03843356,  0.28665154],
       [-0.34062009,  0.79352777],
       [-1.16225216,  0.79350459],
       [ 0.19419328,  1.60986703],
       [ 0.41018415,  1.54828838],
       [-0.61113336,  0.99020048],
       [ 0.08837677,  0.95373644],
       [-1.77183232, -0.12717568],
       [-0.54560628,  1.07613052],
       [-1.69901425,  0.55489764],
       [-0.7449788 ,  0.7519103 ],
       [-1.84473763,  0.55248995],
       [-0.50824943,  1.08964891],
       [-1.35655196,  0.7102918 ],
       [-0.71295569,  0.38030989],
       [ 0.0582823 ,  1.35158484],
       [-2.74743505, -0.18849513],
       [-2.36125827, -0.22542297],
       [ 0.28512568,  1.52124326],
       [-0.67059538,  0.61188467],
       [-1.08310962,  0.57068698],
       [-1.59421684,  0.32055693],
       [-0.58608561,  0.98441983],
       [ 0.91449962,  1.74231742],
       [-1.78271812,  0.25676529],
       [-0.30880495,  0.98633121],
       [-0.80196522,  0.56542478],
       [-1.64551419,  0.2527351 ],
       [ 0.88404065,  1.80009243],
       [ 0.07752252,  1.19103008],
       [ 0.01499115,  1.35642701],
       [-1.37772455,  0.58176578],
       [-0.9893581 ,  0.6000557 ],
       [-0.20708577,  0.97773425],
       [-0.97487675,  0.67788572],
       [-0.84898247,  0.76214066],
       [-2.87107864,  0.01823837],
       [-1.52762479,  0.15224236],
       [-1.19066619,  0.61716677],
       [-0.78719074,  1.22733157],
       [ 0.37887222,  1.38907542],
       [-0.29892079,  1.20534091],
       [-1.21904812,  0.45126808],
       [-0.01954643,  1.00443244],
       [-2.7534539 , -0.41174779],
       [ 0.00290918,  1.19376387],
       [-0.3465645 ,  0.97372693],
       [-0.38706669,  0.98612011],
       [-0.3909804 ,  1.1737113 ],
       [ 0.67985963,  1.57038317],
       [-1.5574845 ,  0.38938231],
       [-0.70276487,  0.84873314],
       [-0.77152456,  1.24328845],
       [-0.78685252,  0.71866813],
       [-1.58251503,  0.47314274],
       [-0.86990291,  1.01246542],
       [-0.76296641,  1.03057172],
       [-1.46908977,  0.50048994],
       [ 0.41590518,  1.35808005],
       [-0.23171796,  0.97466644],
       [-0.35599838,  1.05651836],
       [-1.86300113,  0.31105633],
       [-1.06979785,  0.89343042],
       [ 0.89051152,  1.36968058],
       [-1.64250124,  0.5395521 ],
       [ 0.19072792,  1.39594182],
       [-0.68980859,  1.51412568],
       [-0.66216014,  0.94064958],
       [-1.98324693,  0.36500688],
       [-1.77543305,  0.48759471],
       [ 0.99143992,  1.53242166],
       [-2.03402523,  0.27661546],
       [-0.98138839,  0.86047666],
       [ 0.86594322,  1.60352598],
       [-1.25510995,  0.40788484],
       [-1.28207069,  0.55164356],
       [-0.50983219,  1.05505834],
       [ 0.98003606,  0.56171673],
       [-1.86097117,  0.44004685],
       [-1.09945843,  0.63380337],
       [-1.44294885,  0.18391039],
       [-1.60512757,  0.25456073],
       [ 0.5505329 ,  1.63447114],
       [-1.13622159,  0.87658095],
       [-0.18029101,  0.98458234],
       [-1.48031015,  0.3667454 ],
       [ 0.94295697,  1.51965296],
       [-1.94413955,  0.257857  ],
       [-1.92812486, -0.15406208],
       [-0.28437139,  0.8520255 ],
       [-0.95551392,  0.28517945],
       [-1.44252631,  0.5455637 ],
       [-0.22064889,  1.33439538],
       [-1.52749019,  0.50443876],
       [ 0.757785  ,  0.42124458],
       [-0.49536512,  0.9627005 ]])

The labels: