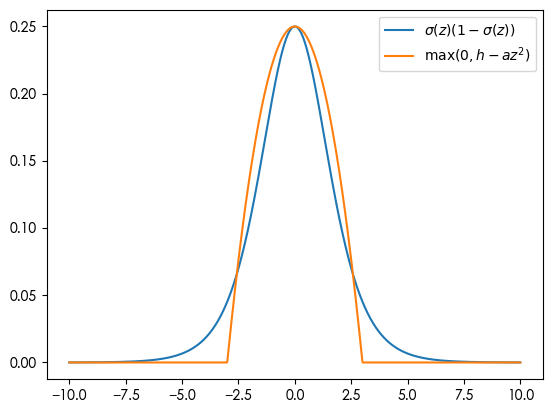
Piecewise quadratic approximation of sigmoid(z) (1-sigmoid(z))

This post shows an approach that approximates $\sigma(z)(1-\sigma(z))$ using piecewise quadratic function, where $\sigma(z)$ is defined to be $1/(1+\exp(-z))$, a.k.a. the sigmoid function.

First, notice that $\sigma(z)(1-\sigma(z)) \approx \log(1+\exp(h - a z^2))$ for certain choice of $h$ and $a$:

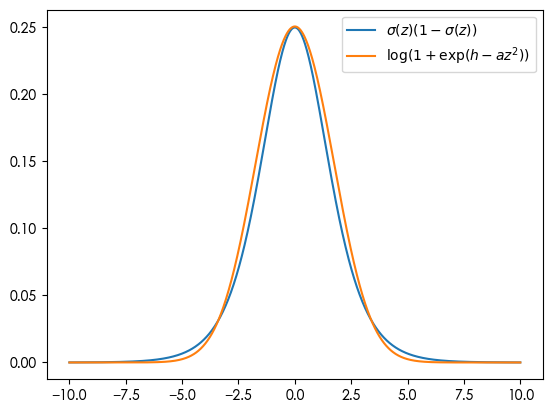
Second, the approximator $\log(1+\exp(\cdot))$ is called a softplus. So it’s natural to proceed: $\log(1+\exp(h - a z^2)) \approx \max(0, h - a z^2)$. Our goal, then, is to choose the height parameter $h$ and width parameter $a$ such that $\sigma(z)(1-\sigma(z)) \approx \max(0, h - a z^2)$.

The height parameter is straightforward to estimate. We need only to match the max of $\sigma(z)(1-\sigma(z))$ to $h$. Hence, $h := \sigma(0)(1-\sigma(0))$.

Noticing that both the original function and the approximator are nonnegative, we may match up their integrals:

\[\int_{-\infty}^\infty \sigma(z)(1-\sigma(z))\,\mathrm d z = \int_{-\infty}^\infty \max(0, h - a z^2)\,\mathrm d z\]

where the left hand side is 1. Plugging in the value of $h$, this equation solves to $a := \frac{16}{9}(\sigma(0)(1-\sigma(0)))^3$.