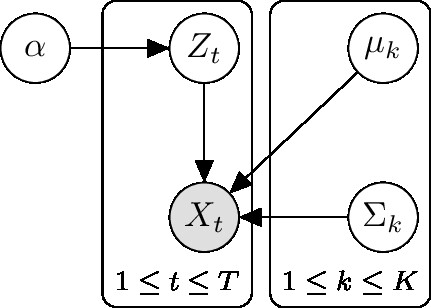
plate diagram of a GMM

plate diagram of a Gaussian Mixture model

The goal is to maximize $\log P(\boldsymbol\Sigma \mid \mathbf x, \boldsymbol\mu,\boldsymbol\alpha)$. $T$ is the number of samples. $K$ is the number of Gaussian components. The dataset is $\mathbf X \triangleq \{\boldsymbol x_t\}_{t=1}^T$.

By expectation-maximization paradigm:

\[\begin{aligned} \log P(\boldsymbol\Sigma \mid \mathbf X, \boldsymbol\mu,\boldsymbol\alpha) &= \log P(\mathbf X \mid \boldsymbol\Sigma,\boldsymbol\mu,\boldsymbol\alpha) + \log P(\boldsymbol\Sigma) + \text{constant}\\ &= \sum_{t=1}^T \log P(\boldsymbol x_t \mid \boldsymbol\Sigma,\boldsymbol\mu,\boldsymbol\alpha) + \log P(\boldsymbol\Sigma) + \text{constant}\\ &= \sum_{t=1}^T \log \sum_{k=1}^K P(\boldsymbol x_t,Z_t=k \mid \boldsymbol\Sigma,\boldsymbol\mu,\boldsymbol\alpha) + \log \sum_{k=1}^K P(\boldsymbol\Sigma_k) + \text{constant}\\ &\ge \sum_{t=1}^T \sum_{k=1}^K P(Z_t=k \mid \mathbf X) \log \left[ \frac{P(\boldsymbol x_t, Z_t=k \mid \boldsymbol\Sigma,\boldsymbol\mu,\boldsymbol\alpha)}{P(Z_t=k \mid \mathbf X)} \right] + \sum_{k=1}^K \log P(\boldsymbol\Sigma_k)\,.\\ \end{aligned}\]

It’s straightforward to compute $P(Z_t=k \mid \mathbf X)$ using Bayes law at E-step. Denote it as $r_{tk}$. The part we need to maximize at M-step is:

\[Q(\boldsymbol\Sigma,\boldsymbol\mu,\boldsymbol\alpha) = \sum_{t=1}^T \sum_{k=1}^K r_{tk} [\log P(Z_t=k \mid \boldsymbol\alpha) + \log \mathcal N(\boldsymbol x_t \mid \boldsymbol\Sigma_k,\boldsymbol\mu_k)] + \sum_{k=1}^K \log P(\boldsymbol\Sigma_k)\,.\]

Note that

\[\log\mathcal N(\boldsymbol x_t \mid \boldsymbol\Sigma_k,\boldsymbol\mu_k) = \frac{1}{2}\log\det \boldsymbol\Sigma_k^{-1} - \frac{1}{2}(\boldsymbol x_t-\boldsymbol\mu_k)^\top \boldsymbol\Sigma_k^{-1} (\boldsymbol x_t-\boldsymbol\mu_k) + \text{constant}\,,\]

that we’ll not focus on the MLE of $\boldsymbol\alpha$ (by Lagrangian multiplier) and $\boldsymbol\mu$, and that the optimization for different $k$’s are independent, we may further simplify the equation to

\[Q(\boldsymbol\Sigma_k) = \sum_{t=1}^T r_{tk} \left[ \frac{1}{2}\log\det \boldsymbol\Sigma_k^{-1} - \frac{1}{2}(\boldsymbol x_t-\boldsymbol\mu_k)^\top \boldsymbol\Sigma_k^{-1}(\boldsymbol x_t-\boldsymbol\mu_k) \right] + P(\boldsymbol\Sigma_k)\,.\]

Using properties of the trace operator,

\[Q(\boldsymbol\Sigma_k) = \frac{1}{2}\sum_{t=1}^T r_{tk} [\log\det \boldsymbol\Sigma_k^{-1} - \operatorname{tr}(\mathbf S_{tk} \boldsymbol\Sigma_k^{-1})] + P(\boldsymbol\Sigma_k)\,,\]

where $S_{tk} \triangleq (\boldsymbol x_t-\boldsymbol\mu_k)(\boldsymbol x_t-\boldsymbol\mu_k)^\top$. For the conjugate prior $P(\boldsymbol\Sigma_k)$, we choose the inverse Wishart distribution:

\[\operatorname{IW}(\boldsymbol\Sigma_k \mid \mathbf S_0^{-1},\nu_0) \propto (\det \boldsymbol\Sigma_k)^{-N_0/2}\exp\left(-\frac{1}{2}\operatorname{tr}(\mathbf S_0 \boldsymbol\Sigma_k^{-1})\right)\,,\]

where $N_0 \triangleq \nu_0 + D + 1$, and $D$ be the dimension of $\boldsymbol x_t$. Thus,

\[Q(\boldsymbol\Sigma_k) = \frac{1}{2}\sum_{t=1}^T r_{tk} [\log\det \boldsymbol\Sigma_k^{-1} - \operatorname{tr}(\mathbf S_{tk} \boldsymbol\Sigma_k^{-1})] + \frac{1}{2}[N_0 \log\det \boldsymbol\Sigma_k^{-1} - \operatorname{tr}(\mathbf S_0 \boldsymbol\Sigma_k^{-1})]\,.\]

Computing the partial derivative of $Q$ with respect to $\Sigma_k^{-1}$ and equating the partial derivative to zero, we have:

\[\begin{aligned} 0 &= \frac{\partial Q}{\partial \boldsymbol\Sigma_k^{-1}}\\ &= \frac{1}{2}\sum_{t=1}^T r_{tk} (\boldsymbol\Sigma_k^\top - \mathbf S_{tk}^\top) + \frac{1}{2} (N_0 \boldsymbol\Sigma_k^\top - \mathbf S_0^\top)\\ &= \frac{1}{2} \sum_{t=1}^T r_{tk} (\boldsymbol\Sigma_k-\mathbf S_{tk}) + \frac{1}{2}(N_0 \boldsymbol\Sigma_k-\mathbf S_0)\\ \boldsymbol\Sigma_k &= \frac{\mathbf S_0 + \sum_{t=1}^T r_{tk} \mathbf S_{tk}}{N_0 + \sum_{t=1}^T r_{tk}}\,.\\ \end{aligned}\]

Further reading:

Section 4.6.2 and 11.4.2.8 of: Kevin P Murphy. Machine learning: a probabilistic perspective. MIT press, 2012.